5 Steps to Excel Integration with Simpson's Rule

Understanding the intricacies of numerical integration methods like Simpson's Rule can significantly enhance your skills in data analysis. Whether you're an engineer, physicist, or someone interested in computational finance, knowing how to integrate functions efficiently can be a game-changer. Here are five steps to seamlessly integrate Simpson's Rule into Excel, providing you with a powerful tool for numerical integration.

1. Setting Up Your Excel Sheet

The first step in integrating Simpson’s Rule in Excel is setting up your spreadsheet. Here’s how you do it:

• Create Columns: Label the columns as A to H. A for data points, B for X values, C for Y values, D for Δx, E for Y_2i, F for Y_2i+1, G for Y_2i+2, and H for the total area calculation.
• Data Entry: In column A, enter the number of intervals or data points you wish to use. Ensure the number is even for Simpson’s Rule to apply correctly.
• Enter X Values: In column B, enter the X values, ensuring the step size (Δx) is constant.
• Enter Y Values: In column C, input the function values corresponding to the X values in column B.

2. Calculating Δx

Once your data is set up, calculate the step size (Δx) for your integration:

• Formula: In cell D2, enter the formula =B2-B1 to get Δx. Copy this formula down the column for all rows.
• Verify Consistency: Ensure Δx is consistent throughout, as Simpson’s Rule requires evenly spaced intervals.

3. Applying Simpson’s Rule

Now, let’s apply Simpson’s Rule:

• Y_2i and Y_2i+2: In column E and G, input the values from column C, skipping every other row. This aligns with Simpson’s Rule where Y_even and Y_even+2 are summed differently.
• Y_2i+1: In column F, input the values from column C, selecting every odd-indexed value. These are multiplied by 4 in Simpson’s Rule.
• Formula: In cell H2, enter the Simpson’s Rule formula:

  =D2 * (C2/3 + 4 * C3/3 + C4/3)
          

  Copy this formula down the column to calculate the area under each segment.

🔍 Note: Simpson’s Rule is an approximation technique, so the result will have an error. The smaller the interval (Δx), the more accurate your results will be.

4. Summing the Areas

After calculating the area under each segment, sum these areas:

• Sum Formula: In the last cell of column H, enter =SUM(H2:H[n]), where [n] is the last row number.
• Result: This sum represents the total area or the integral of your function using Simpson’s Rule.

5. Verifying Results and Error Analysis

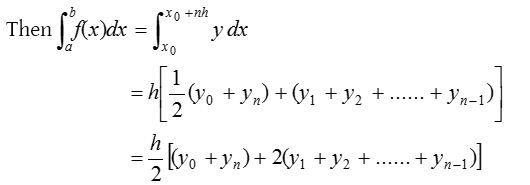
It’s crucial to ensure the accuracy of your integration results:

• Compare Results: If possible, compare your results with known analytical solutions or different numerical methods like the Trapezoidal Rule or integration using other tools.
• Error Estimation: Use the Maxima or MATLAB software to check the true value of the integral if known. Calculate the absolute and relative error as follows:
  • Absolute Error: |True Value - Calculated Value|
  • Relative Error: (Absolute Error / True Value) * 100%
• Adjust Intervals: If errors are high, reduce the interval size or check your data for accuracy.

In this journey through numerical integration, we’ve learned how to integrate Simpson’s Rule into Excel, providing a robust tool for calculating integrals in various fields. From setting up the spreadsheet to calculating, summing areas, and verifying results, each step enhances your capability to handle complex data analysis. This method, when used correctly, can offer high accuracy in integration, especially useful when dealing with smooth, continuous functions. Remember, the quality of your input data and the appropriateness of Simpson’s Rule to your problem are key to obtaining reliable results.

What is Simpson’s Rule?

+

Simpson’s Rule is a numerical method for approximating the definite integral of a function. It uses parabolic arcs to estimate the area under the curve, providing more accuracy than simpler methods like the Trapezoidal Rule.

Why use Simpson’s Rule in Excel?

+

Excel is widely accessible, and integrating Simpson’s Rule allows for quick numerical integrations for data analysis, especially when dealing with complex datasets or functions for which analytical solutions are cumbersome.

Can I use Simpson’s Rule for any function?

+

Simpson’s Rule works best with smooth, continuous functions. For functions with discontinuities or sharp changes, other integration methods might be more suitable.